
The appropriate type of control chart depends on the classification of the data, type of underlying distribution and intent of application. The major difference between 2 sigma vs 3 sigma control charts are that the former finds ways to detect small shifts from the standard deviation but not necessarily signifying process instability whereas, the latter finds application to detect medium to large shifts in data from the mean. 2 sigma limits are, however, insufficient to ascertain process stability, and as such, 2 sigma control charts show only if there is a requirement to ascertain extremely sensitive process deviation. Such charts make use of historical data points and detect small shifts of 1 sigma and 2 sigma levels.
A time-weighted 2-sigma control chart is an alternative to the Shewhart-type 3-sigma charts. Previous observations do not influence the probability of future out-of-control signals. These charts have a major drawback of having no memory and using only the last plotted data. Three-sigma Shewhart-type control charts effectively detect medium to large shifts in data but are also insensitive to small shifts of data.

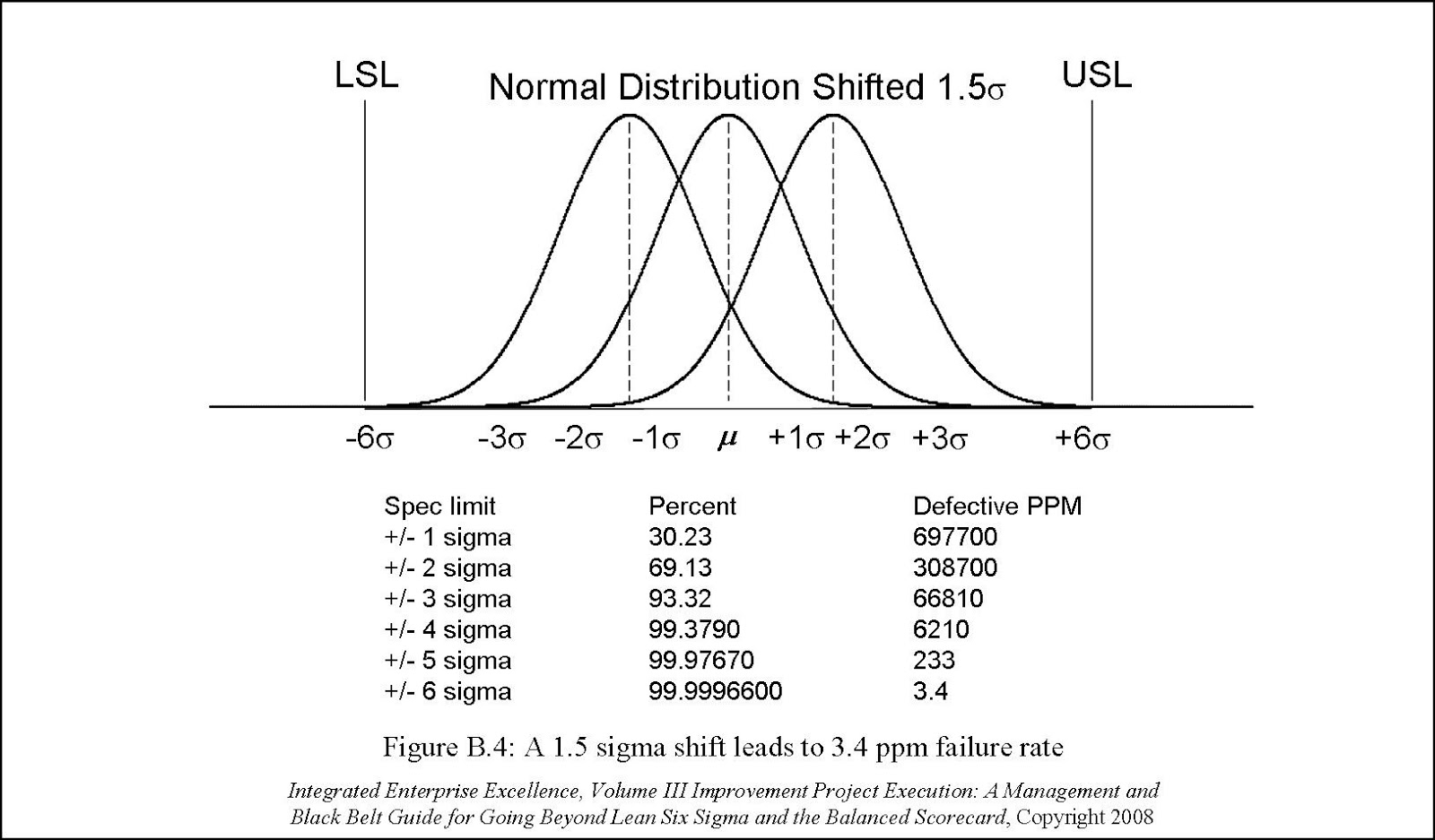
Statistical Performance of 2 Sigma vs 3 Sigma Control Charts For this exact reason, the traditional control chart formulated by Walter Shewhart in 1924 and most control charts since have used 3-sigma limits to test the deviance of data. A process attains stability when data in the control chart falls within 3-sigma limits from the standard deviation. In statistical control, 1 sigma is the lowest sigma and 6 sigma the highest. A 2 sigma control limit, therefore, indicates the extent to which data deviates from the 95% probability, and a 3 sigma control limit indicates the extent to which the defects deviate from the acceptable 1,350 defects. Three sigma limits indicate data chosen randomly from a set of normally distributed data and has a 99.73% of probability of being within the acceptable standard deviation, translating into a possibility of 1,350 defects per million opportunities. Two sigma limits indicate data chosen randomly from a set of normally distributed data that has a 95% of probability of being within the acceptable standard deviation.

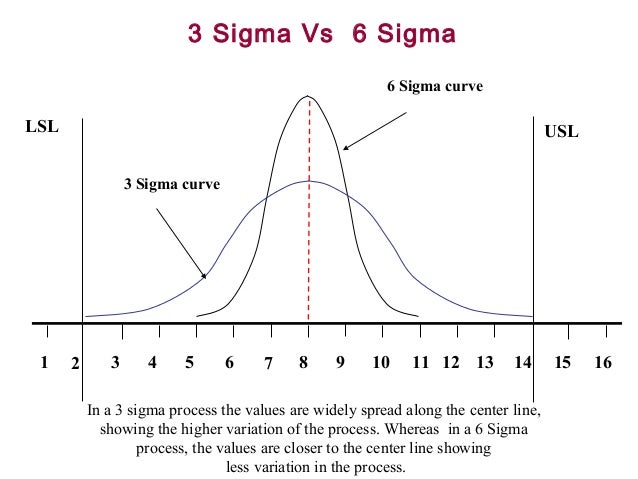
A smaller sigma level denotes less variability, or close data points. Sigma is the measure of standard deviation or, the extent to which data can vary in a given distribution. Learn the difference between 2 sigma and 3 sigma charts 2 sigma limits and 3 sigma limits are indicators of the accuracy of the measurement method used in control charts. This article will explain the differences between 2 Sigma and 3 Sigma control charts. When the data from the control chart indicates variation in process quality, due to both random and special causes, the process is out of control. Control charts help achieve and maintain process stability by identifying the state where the process displayed consistency in the past and expects to do so in the future. A control chart is a quality control tool that determines whether a manufacturing or business process is in a state of statistical control.


 0 kommentar(er)
0 kommentar(er)
